Input-Output Models as Graph Networks

We discuss the relation of economic input-output models with graph theory and networks

Equinox
Reading Time: 1 min.

Course Objective

The objective of the course is to discuss the relation of economic input-output models with graph theory and networks.

The course is now live at the Academy.

Pre-requisites

Basic knowledge of input-output models and graph theory would help to get the most out of the course but is not strictly required.

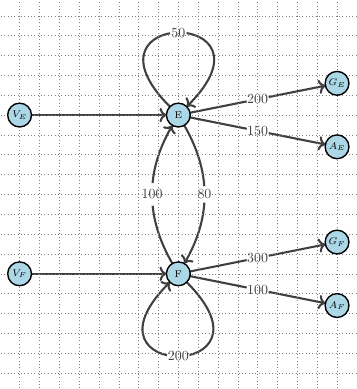
Summary of the Course

What we cover in this course:

  • Step 1. In this step we discuss in more detail the motivation for the course and provide a very brief introduction to the graph theory to establish the notation.
  • Step 2. In this step we explore the duality between graphs and matrix representations.
  • Step 3. This step introduces the concept of Qualitative Input-Output Analysis
  • Step 4. In the fourth step off the course we discuss Sources, Sinks and Conservation Laws
  • Step 5.In the final step of the course discuss and interpret in graph terms the typical question one wants to answer with an IO model: what happens if there is new set of final demands?

Get Started with the Course

IO Graph

The course is available at the Academy.