Open Source Securitisation

Releases, Open Source Tools
Reading Time: 5 min.
Page content

Open Source Securitisation

Motivation

After the Great Financial Crisis securitisation has become the poster child of a financial product exhibiting complexity and opaqueness. The issues and lessons learned post-crisis were many, involving all aspects of the securitisation process, from the nature and quality of the underlying assets, the incentives of the various agents involved and the ability of investors to analyze the products they invested in. While the most egregious complications involved various types of re-securitisation and/or the interplay of structured credit derivatives undoubtedly even vanilla securitisation structure has a considerable amount of business logic.

An important recent initiative in the European Union aims to enable a market for a new type of securitisation (STS, Simple, Transparent and Standardized Securitisation) that has the potential to restart this particular financing channel in the EU on a more healthy and sustainable basis, complementing initiatives covering the banking channel.

A major component of that initiative as it is being implemented in European law is adequate disclosure of the nature and risks of underlying exposures. In particular there are now detailed ESMA templates per asset class.

Next to the asset side, investor due-diligence requires to examine on the liability side, quote:

all the structural features of the securitisation that can materially impact the performance of the securitisation position, including the contractual priorities of payment and priority of payment-related triggers, credit enhancements, liquidity enhancements, market value triggers, and transaction-specific definitions of default

Too complex to perceive?

While proper due diligence requires examining the structure closely, a casual inspection of offering circulars of securitisations and similar products suggests significant complexity, especially as elaborate logical sequences are expressed solely in terms of words over hundreds of pages

In the article Too Complex to Perceive? Drafting Cash

Distribution Waterfalls Directly as Code to Reduce Complexity and Legal Risk in Structured Finance Ralph C. Mayrell ever argues that the functional code that creates the functional reality of the securisation should become the contract by reference in the legal deal document and thus should become the legally determinative reality. This would reduce the confusion that impedes perception of the future reality of the financial product’s cash flow distributions

While the requirement to have code as legal contract might be premature for some, using technical means to pin down the actual nature of the securitisation contract is a very opportune direction and in line with the objectives of STS. In fact even a self contained mathematical description of the structure and its contingent behavior is a significant step towards clarity (see Chapter 10: Toward market-implied valuations of cash-flow CLO structures, P. Papadopoulos in Credit Risk Frontiers, Subprime crisis, pricing, and hedging, CVA, MBS, Ratings and Liquidity, Bloomberg 2011, Editors: Bielecki, Brigo, Patras)

Approach

Our proposal for Open Source Securitisation rests on technology, standards and practices that are fairly common in other IT sectors and can be adopted in this domain as well. We use a toolkit around the popular Python language but implementations in other languages are possible. There are three core elements:

  • A declarative specification of the securitisation structure
  • A declarative specification of cash flow distributions
  • An implementation in code of the cash flow payments logic

Declarative specification of the securitisation structure

The objective here is to have a representation of the securitisation structure that is at the same time human readable and interpretable as code. We use for the purpose the YAML standard. An example is included in the file below.

!!python/object:Securitisation.Structure
Equity: !!python/object:Securitisation.Equity
  amount: 0.04999999999999999
  payment: null
FeeStructure: null
IC_Tests:
- !!python/object:Securitisation.IC_Test
  IC_Ratio: null
  IC_Status: null
  IC_Trigger: 1.0
- !!python/object:Securitisation.IC_Test
  IC_Ratio: null
  IC_Status: null
  IC_Trigger: 1.0
- !!python/object:Securitisation.IC_Test
  IC_Ratio: null
  IC_Status: null
  IC_Trigger: 1.0
- !!python/object:Securitisation.IC_Test
  IC_Ratio: null
  IC_Status: null
  IC_Trigger: 1.0
IC_haircut: 0.0
Liabilities:
- !!python/object:Securitisation.Bond
  Bond_Spread: 0.02
  IC_Trigger: 0.0
  Indicator: A1
  Notional: null
  OC_Trigger: 0.0
  Payment: null
  Rank: null
  Type: Senior
  initial_Notional: 0.75
  scheduled_Payment: 0.0
  spread: 0.0
- !!python/object:Securitisation.Bond
  Bond_Spread: 0.05
  IC_Trigger: 0.0
  Indicator: M1
  Notional: null
  OC_Trigger: 0.0
  Payment: null
  Rank: 1
  Type: Mezzanine
  initial_Notional: 0.1
  scheduled_Payment: 0.0
  spread: 0.0
- !!python/object:Securitisation.Bond
  Bond_Spread: 0.1
  IC_Trigger: 0.0
  Indicator: M2
  Notional: null
  OC_Trigger: 0.0
  Payment: null
  Rank: 2
  Type: Mezzanine
  initial_Notional: 0.05
  scheduled_Payment: 0.0
  spread: 0.0
- !!python/object:Securitisation.Bond
  Bond_Spread: 0.15
  IC_Trigger: 0.0
  Indicator: M3
  Notional: null
  OC_Trigger: 0.0
  Payment: null
  Rank: 3
  Type: Mezzanine
  initial_Notional: 0.05
  scheduled_Payment: 0.0
  spread: 0.0
OC_Tests:
- !!python/object:Securitisation.OC_Test
  OC_Ratio: null
  OC_Status: null
  OC_Trigger: 1.2
- !!python/object:Securitisation.OC_Test
  OC_Ratio: null
  OC_Status: null
  OC_Trigger: 1.1
- !!python/object:Securitisation.OC_Test
  OC_Ratio: null
  OC_Status: null
  OC_Trigger: 1.08
- !!python/object:Securitisation.OC_Test
  OC_Ratio: null
  OC_Status: null
  OC_Trigger: 1.01
OC_haircut: 1.0
Tests: 4
adj_notional: null
reserve: !!python/object:Securitisation.Reserve
  amount: 0.0
senior_fees: 0.0025

A declarative specification of cash flow distributions

A key element of the prospectus is the specification of payment rules, connecting various accounts, subject to triggers and availability of funds. These elementary payment transactions can be extracted and documented in separate YAML documents and subsequently used as lambda functions. An example file is shown next:

floating_rate_payment:
    function: "lambda x1, x2, x3: (x1 + x2) *x3"
    description: "Calculate floating rate interest payment"
subtract_amount:
    function: "lambda x1, x2: max(0.0, x1 - x2)"
    description: "Subtract and amount and assign to new variable"
collect_payments:
    function: "lambda x1, x2: x1 + x2"
    description: "Add payments from two sources"
apply_scheduled_payment:
    function: "lambda x1, x2: min(x1, x2)"
    description: "Make payment up to the scheduled amount"
compound_and_add:
function: "lambda x1, x2, x3: (1.0 + x1)* x2 + x3"
    description: "Compound an account with interest and add cashflow"
required_reduction:
  function: "lambda x1, x2,: max(min(x1, x2), 0.0)"
  description: "Calculate required reduction (bounded to be positive)"

Implementing cash flow waterfalls in code

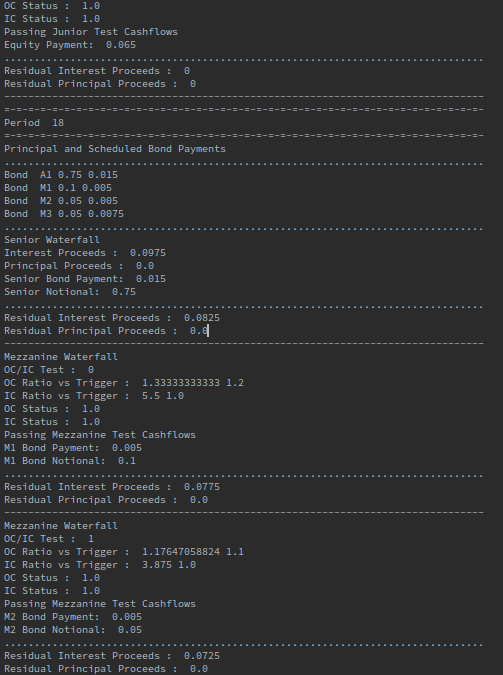
While declarative specification of structural elements goes a long way towards making the structure both well defined and readily analyzable, ultimately the complete and final logic of the structure must be represented using a programming language. In contrast to e.g. spreadsheet solutions that are difficult to validate, a procedural language with well-defined flow of instructions and logical branching points allows unambiguous definition of cash-flows under all contingencies. The following is an excerpt (full script in the repository)

# STEP 2c: IP/PP distributions on the basis of the OC/IC tests
# Case 2c_1: Passing the i-th (OC, IC) test
if OCTest.OC_Status[k] == 1 and ICTest.IC_Status[k] == 1:

# Passing Mezzanine Test
if i < T - 1:
    # Pay available interest in i+1 subordinated note.
    # If there is shortfall, it is added as deferred interest to the bond notional
    # Adjust interest proceeds
    # No changes to the available principal proceeds
    B = S.Liabilities[i + 1]
    B.Payment[k] += F["apply_scheduled_payment"](B.Scheduled_Payment[k], interest_proceeds)
    B.Notional[k] += B.Scheduled_Payment[k] - B.Payment[k]
    interest_proceeds = max(0.0, interest_proceeds - B.Payment[k])
    print('Passing Mezzanine Test Cashflows')
    print(B.Indicator, "Bond Payment: ", B.Payment[k])
    print(B.Indicator, "Bond Notional: ", B.Notional[k])
# Passing Junior Test
else:
    # Allocation of all proceeds to reserve account (if any)
    # Make equity payments
    S.reserve.amount = F["compound_and_add"](A.r, S.reserve.amount, principal_proceeds)
    principal_proceeds = 0
    S.Equity.payment[k] = interest_proceeds
    interest_proceeds = 0
    print('Passing Junior Test Cashflows')
    print("Equity Payment: ", S.Equity.payment[k])

Demonstration

In our GitHub repository we have a demo implementation that aims to illustrate the proposal in sufficient detail. The demo does not represent any specific / actual structure, it merely abstracts features commonly found in existing structures: (multiple bonds with priority of payments, principal and interest payment waterfalls, reserve accounts, overcollatelarization triggers etc.)

Cashflows