Connecting the Dots, Tensor Representations of Activitypub Networks

What are ActivityPub Networks?

ActivityPub is a technical specification towards decentralized (more precisely, federated) social networking (termed the Fediverse) based upon the exchange of ActivityStreams messages that follow the Activity Vocabulary. The ActivityPub proposal has been standardized and published by the W3C and has motivated the design of several federated social networking systems.

There are presently several concrete ActivityPub compliant implementations and the protocol sees meaningful adoption, primarily in the domain of federated social networks. Current ActivityPub networks consist of several million individual users, using several thousands of distinct servers, and a few dozens of distinct server types. An overview of ongoing network statistics is available here.

Different ActivityPub server types might target a variety of use cases, or simply reflect different underlying technologies. Use cases include exchanges of smaller or larger pieces of text (termed Microblogging/Blogging), cataloging and reviewing of Books, Podcasting, the creation and sharing of Images or Videos, shared Calendar and Event Planning applications, Music Hosting, Bookmark or Link Aggregators, Discussion Forums and more. Federation of collaborative software development activities (based on the git paradigm and tools) is another important work-in-progress.

NB: As Open Risk we are already present on the Fediverse via a Mastodon account.

Connecting the Dots of Online Networks

Analysing and understanding the dynamics of economic networks is of vital importance for informed decision-making. In a number of previous White Papers we reviewed and illustrated how mathematical concepts from Network and Graph theory (OpenRiskWP08,OpenRiskWP10).

Our focus in the latest White Paper (OpenRiskWP15) in the Connect the Dots series is on mathematical (in particular Tensor) representations of federated online networks that help encode succinctly certain important elements of their structure. We focus on federated networks adhering to the ActivityPub protocol, which we discuss in the relevant detail.

The Main Ideas

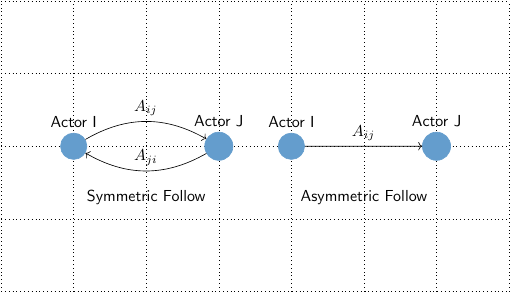
The classic, simple (with no self-loops), directed graph is sufficient to describe the Following/Followed connectivity of Actors within a single Server. The core idea is to map Actors to graph nodes, and express relations using graph edges.

This model can be useful to analyze sub-graphs of a network, in particular if the Server instance is large with many users. The benefit of using a simple graph is that one can directly map its structure into matrix notation and then use the well-developed machinery or linear algebra. The challenge is that actual ActivityPub networks will be quite a bit more demanding in the variety of Actor and Activities that they engage in, which limits the utility of simple graphs.

Multiple Servers of the Same type

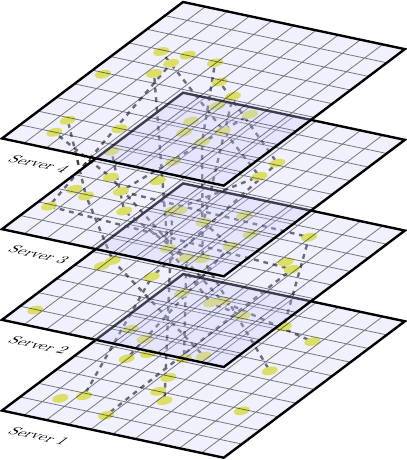
The first complication is that the network will involve multiple servers, potentially a very large number indeed. The Server-to-Server layer is made up of all interconnected Servers (Server N) with a varying amount of user / Actors (from one to very many). The actual social network layer is formed by the follow relationships between these Actors (User K @ Server N) hosted by different Servers.

Loosely speaking, Tensors can be seen as generalizations of vectors and matrices. Vectors could be called rank-1 tensors, they have one index. Matrices are rank-2 tensors, they have two indexes or dimensions. The more indices, the higher the rank of a tensor. Adjacency Matrices are rank-2 tensors, so they are inherently limited in the complexity of the relationships they can capture.

Adjacency Tensors are higher-order objects that can potentially capture more complex network relations. The multilayer adjacency tensor $A$ is a very general object that can be used to represent a wealth of complicated relationships among nodes.

The simplest generalization of an Adjacency Tensor beyond an Adjacency Matrix would be the fourth-order, or rank-4, tensor $A^{ab}_{ij}$ where the indices $(a,b)$ range over a single additional layer dimension (e.g., a count of Server instances) and $(i, j)$ ranges over the nodes (e.g. Actors).

$$ A^{ab}_{ij} = \left \{ \begin{array}{r@{\quad : \quad}l} 1 & \mbox{if link from node} , (i,a) , \mbox{to node} , (j,b) \\ 0 & \mbox{otherwise} \end{array} \right. $$

In the case of multiple ActivityPub servers we might use the extra dimension to range of the different instances.

Servers of Different Type

A second complicating dimension is that the network will involve servers of different types (which for example are able to exchange and process a different subset of messages).

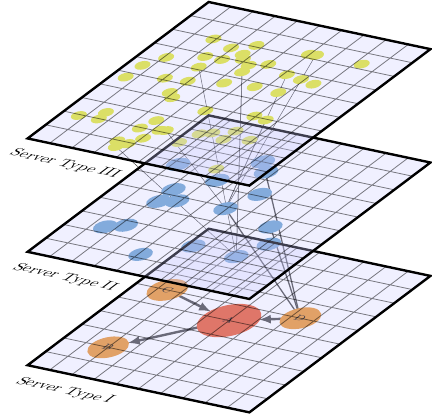
These two facets of a minimal multilayer network representation that resolves both Server types and individual Server instances can be put together in the following rank-6 Tensor:

$$ A^{abkl}_{ij} = \left \{ \begin{array}{r@{\quad : \quad}l} 1 & \mbox{if link from node} , (i, a, k) , \mbox{to node} , (j, b, l) \\ 0 & \mbox{otherwise} \end{array} \right. $$

This object is then the starting point for a variety of possible tasks.

What are those formulations good for?

Graph theoretic representations of ActivityPub networks have already been used recently to enable the consistent capture (data modeling) and statistical analysis of public fediverse data. Another motivation is enabling the theoretical modeling and simulation of ActivityPub network properties and behaviors. The mapping of networks to tensor algebra is typically the first step in that process. Depending on the task one might need to flatten the relevant tensors into the so-called supra-adjacency matrix which can then be analysed with more conventional matrix algebra.